Wilson loop and Wilczek-Zee phase from a non-Abelian gauge field

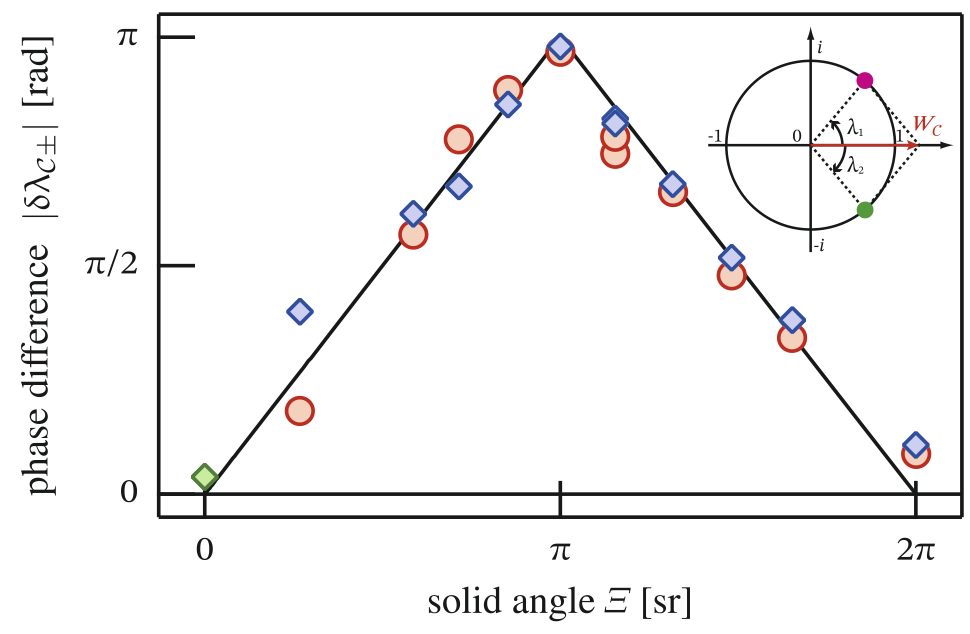
Quantum states can acquire a geometric phase called the Berry phase after adiabatically traversing a closed loop, which depends on the path not the rate of motion. The Berry phase is analogous to the Aharonov–Bohm phase derived from the electromagnetic vector potential, and can be expressed in terms of an Abelian gauge potential called the Berry connection. Wilczek and Zee extended this concept to include non-Abelian phases—characterized by the gauge-independent Wilson loop—resulting from non-Abelian gauge potentials. Using an atomic Bose–Einstein condensate, we quantum-engineered a non-Abelian SU(2) gauge field, generated by a Yang monopole located at the origin of a 5-dimensional parameter space. By slowly encircling the monopole, we characterized the Wilczek–Zee phase in terms of the Wilson loop, that depended on the solid-angle subtended by the encircling path: a generalization of Stokes’ theorem. This observation marks the observation of the Wilson loop resulting from a non-Abelian point source.