Imaging topology of Hofstadter ribbons
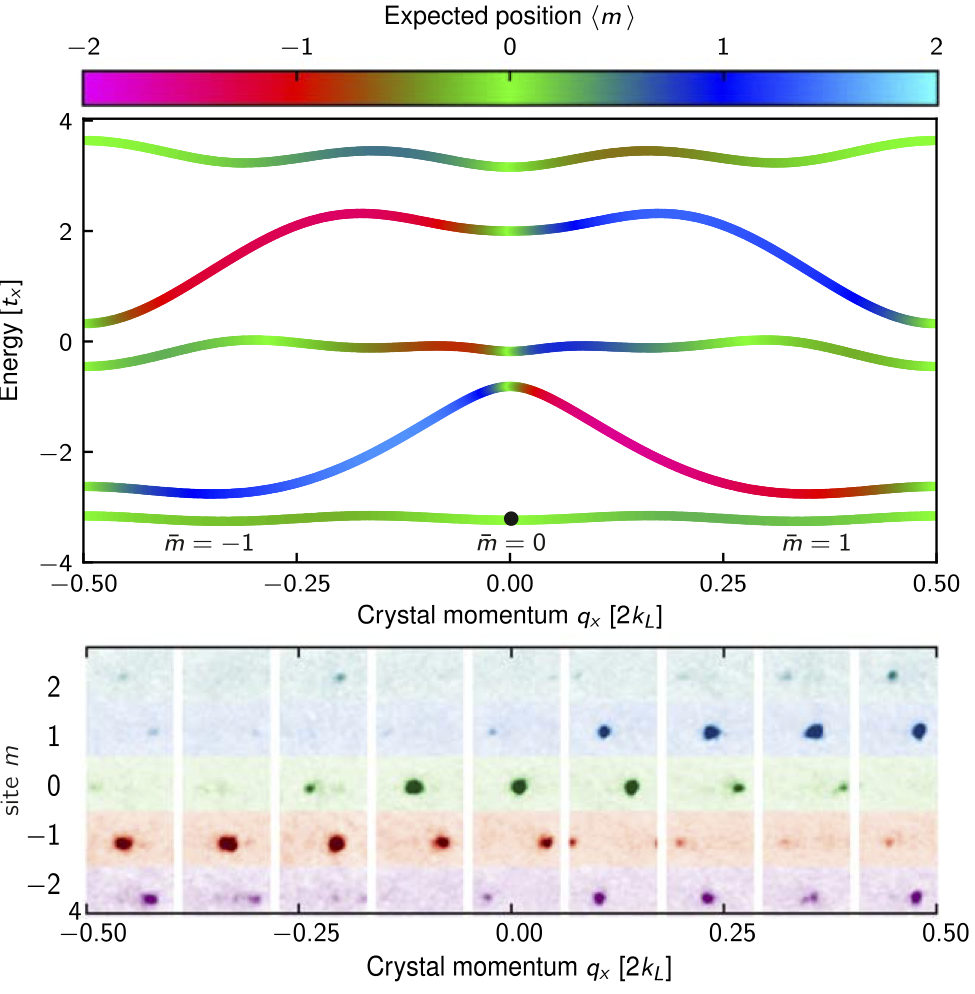
Physical systems with non-trivial topological order find direct applications in metrology (Klitzing et al 1980 Phys. Rev. Lett. 45 494–7) and promise future applications in quantum computing (Freedman 2001 Found. Comput. Math. 1 183–204; Kitaev 2003 Ann. Phys. 303 2–30). The quantum Hall effect derives from transverse conductance, quantized to unprecedented precision in accordance with the system’s topology (Laughlin 1981 Phys. Rev. B 23 5632–33). At magnetic fields beyond the reach of current condensed matter experiment, around 10^4 T, this conductance remains precisely quantized with values based on the topological order (Thouless et al 1982 Phys. Rev. Lett. 49 405–8). Hitherto, quantized conductance has only been measured in extended 2D systems. Here, we experimentally studied narrow 2D ribbons, just 3 or 5 sites wide along one direction, using ultracold neutral atoms where such large magnetic fields can be engineered (Jaksch and Zoller 2003 New J. Phys. 5 56; Miyake et al 2013 Phys. Rev. Lett. 111 185302; Aidelsburger et al 2013 Phys. Rev. Lett. 111 185301; Celi et al 2014 Phys. Rev. Lett. 112 043001; Stuhl et al 2015 Science 349 1514; Mancini et al 2015 Science 349 1510; An et al 2017 Sci. Adv. 3). We microscopically imaged the transverse spatial motion underlying the quantized Hall effect. Our measurements identify the topological Chern numbers with typical uncertainty of 5%, and show that although band topology is only properly defined in infinite systems, its signatures are striking even in nearly vanishingly thin systems
Imaging topology of Hofstadter ribbons ; D. Genkina, L. M. Aycock, H.-I. Lu, M. Lu, A. M. Pineiro, and I. B. Spielman; New Journal of Physics 21 053021 (2019). doi:10.1088/1367-2630/ab165b
https://iopscience.iop.org/article/10.1088/1367-2630/ab165b/meta
