Scale-Invariant Continuous Entanglement Renormalization of a Chern Insulator
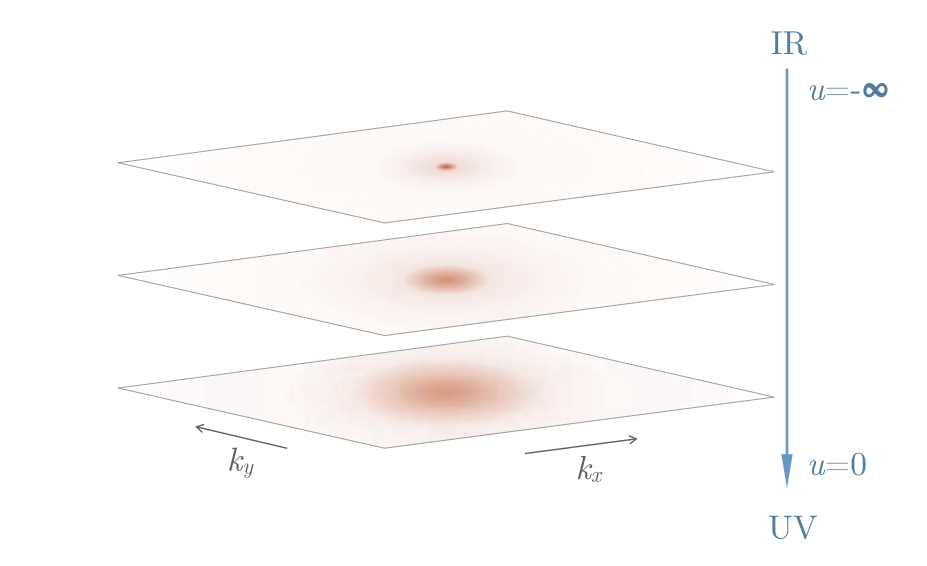
The multiscale entanglement renormalization ansatz (MERA) postulates the existence of quantum circuits that renormalize entanglement in real space at different length scales. Chern insulators, however, cannot have scale-invariant discrete MERA circuits with a finite bond dimension. In this Letter, we show that the continuous MERA (cMERA), a modified version of MERA adapted for field theories, possesses a fixed point wave function with a nonzero Chern number. Additionally, it is well known that reversed MERA circuits can be used to prepare quantum states efficiently in time that scales logarithmically with the size of the system. However, state preparation via MERA typically requires the advent of a full-fledged universal quantum computer. In this Letter, we demonstrate that our cMERA circuit can potentially be realized in existing analog quantum computers, i.e., an ultracold atomic Fermi gas in an optical lattice with light-induced spin-orbit coupling.
Scale-Invariant Continuous Entanglement Renormalization of a Chern Insulator ; S.-K. Chu, G. Zhu, J. R. Garrison, Z. Eldredge, A. V. Curiel, P. Bienias, I. B. Spielman, and A. V. Gorshkov; Phys. Rev. Lett. 122 120502 (2019). doi:10.1103/PhysRevLett.122.120502
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.120502
