Dynamical structure factor from weak measurements

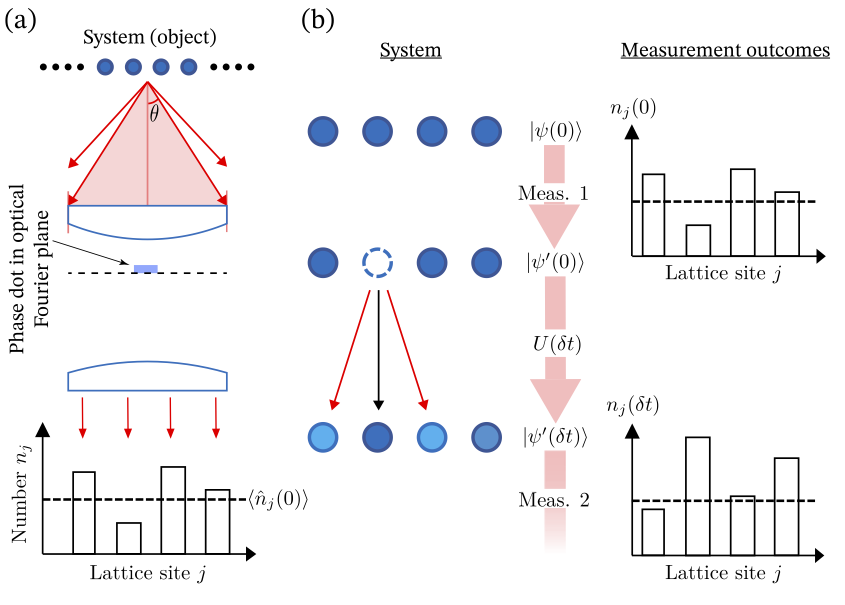
Much of our knowledge of quantum systems is encapsulated in the expectation value of Hermitian operators, experimentally obtained by averaging projective measurements. However, dynamical properties are often described by products of operators evaluated at different times; such observables cannot be measured by individual projective measurements, which occur at a single time. For example, the dynamical structure factor (DSF) describes the propagation of density excitations, such as phonons, and is derived from the spatial density operator evaluated at different times. In equilibrium systems this can be obtained by first exciting the system at a specific wavevector and frequency, then measuring the response. Here, we describe an alternative approach using a pair of time-separated weak measurements, and analytically show that their cross-correlation function directly recovers the DSF, for all systems, even far from equilibrium. This general schema can be applied to obtain the cross-correlation function of any pair of weakly observable quantities. We provide numerical confirmation of this technique with a matrix product states simulation of the one-dimensional Bose–Hubbard model, weakly measured by phase contrast imaging. We explore the limits of the method and demonstrate its applicability to real experiments with limited imaging resolution.