Enhanced transport of spin-orbit-coupled Bose gases in disordered potentials

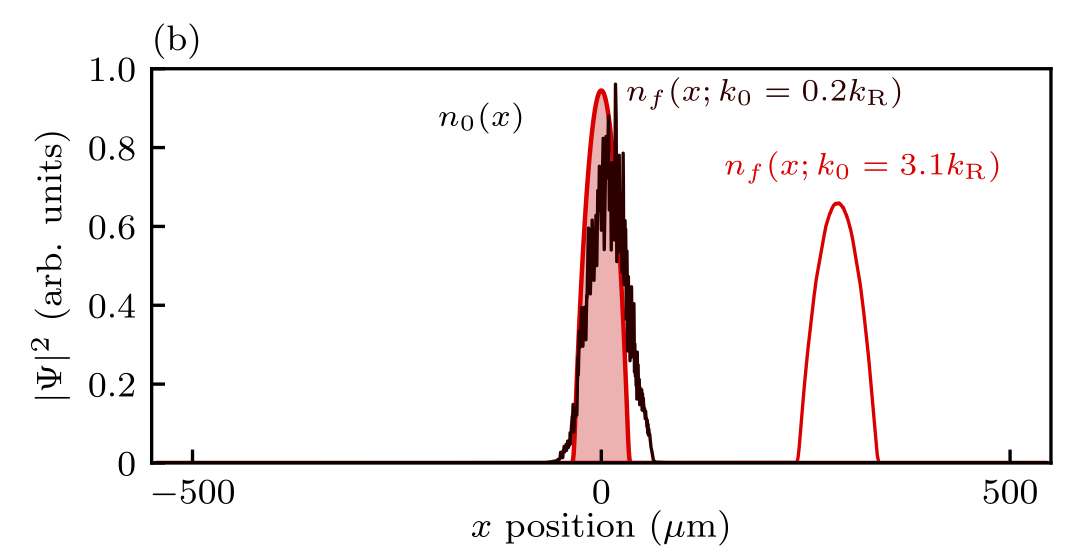
Anderson localization is a single-particle localization phenomena in disordered media that is accompanied by an absence of diffusion. Spin-orbit coupling (SOC) describes an interaction between a particle’s spin and its momentum that directly affects its energy dispersion, for example, creating dispersion relations with gaps and multiple local minima. We show theoretically that combining one-dimensional spin-orbit coupling with a transverse Zeeman field suppresses the effects of disorder, thereby increasing the localization length and conductivity. This increase results from a suppression of backscattering between states in the gap of the SOC dispersion relation. Here, we focus specifically on the interplay of disorder from an optical speckle potential and SOC generated by two-photon Raman processes in quasi-one-dimensional Bose-Einstein condensates. We first describe backscattering by using a Fermi golden rule approach, and then numerically confirm this picture by solving the time-dependent one-dimensional Gross–Pitaevskii equation for a weakly interacting Bose-Einstein condensate with SOC and disorder. We find that on the tens of millisecond timescale of typical cold atom experiments moving in harmonic traps, initial states with momentum in the zero-momentum SOC gap evolve with negligible backscattering, while without SOC these same states rapidly localize.

Enhanced transport of spin-orbit-coupled Bose gases in disordered potentials; . Yue, C. A. R. Sá de Melo, and I. B. Spielman; Phys. Rev. A 102 102 033325 (2020). doi:10.1103/PhysRevA.102.033325

https://journals.aps.org/pra/abstract/10.1103/PhysRevA.102.033325