Brownian motion of solitons in a Bose–Einstein condensate

Solitons, spatially localized, mobile excitations resulting from an interplay between nonlinearity and dispersion, are ubiquitous in physical systems from water channels and oceans to optical fibers and Bose–Einstein condensates (BECs). From our pulse throbbing at our wrists to rapidly moving tsunamis, solitons appear naturally at a wide range of scales. In nonlinear optical fibers, solitons can travel long distances with applications for communication technology and potential for use in quantum switches and logic. Understanding how random processes contribute to the decay and the diffusion of solitons is essential to advancing these technologies.

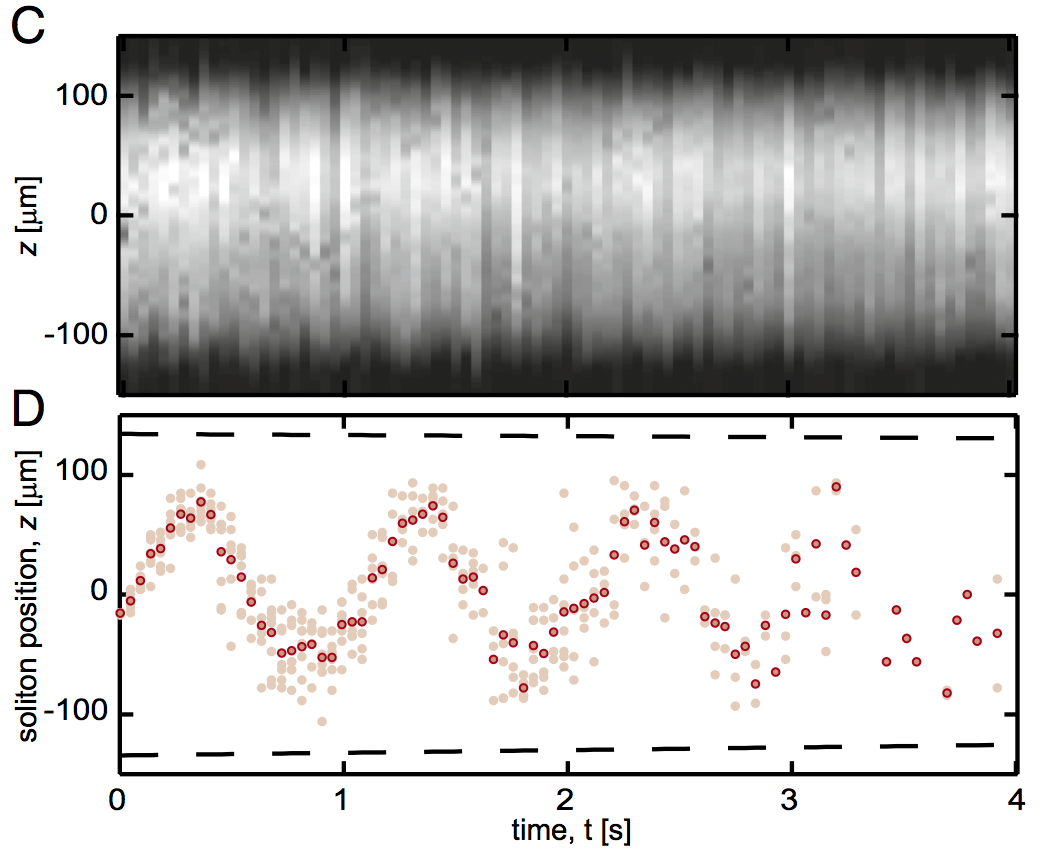
We observed and controlled the Brownian motion of solitons. We launched solitonic excitations in highly elongated Rb87 Bose–Einstein condensates (BECs) and showed that a dilute background of impurity atoms in a different internal state dramatically affects the soliton. With no impurities and in one dimension (1D), these solitons would have an infinite lifetime, a consequence of integrability. In our experiment, the added impurities scatter off the much larger soliton, contributing to its Brownian motion and decreasing its lifetime. We describe the soliton’s diffusive behavior using a quasi-1D scattering theory of impurity atoms interacting with a soliton, giving diffusion coefficients consistent with experiment.

http://www.pnas.org/content/early/2017/02/13/1615004114.abstract

Brownian motion of solitons in a Bose–Einstein condensate; L. M. Aycock, H. M. Hurst, D. K. Efimkin, D. Genkina, H.-I. Lu, V. M. Galitski, and I. B. Spielman; Proceedings of the National Academy of Sciences (2017). doi:10.1073/pnas.1615004114