Interference induced anisotropy in a two-dimensional dark state optical lattice

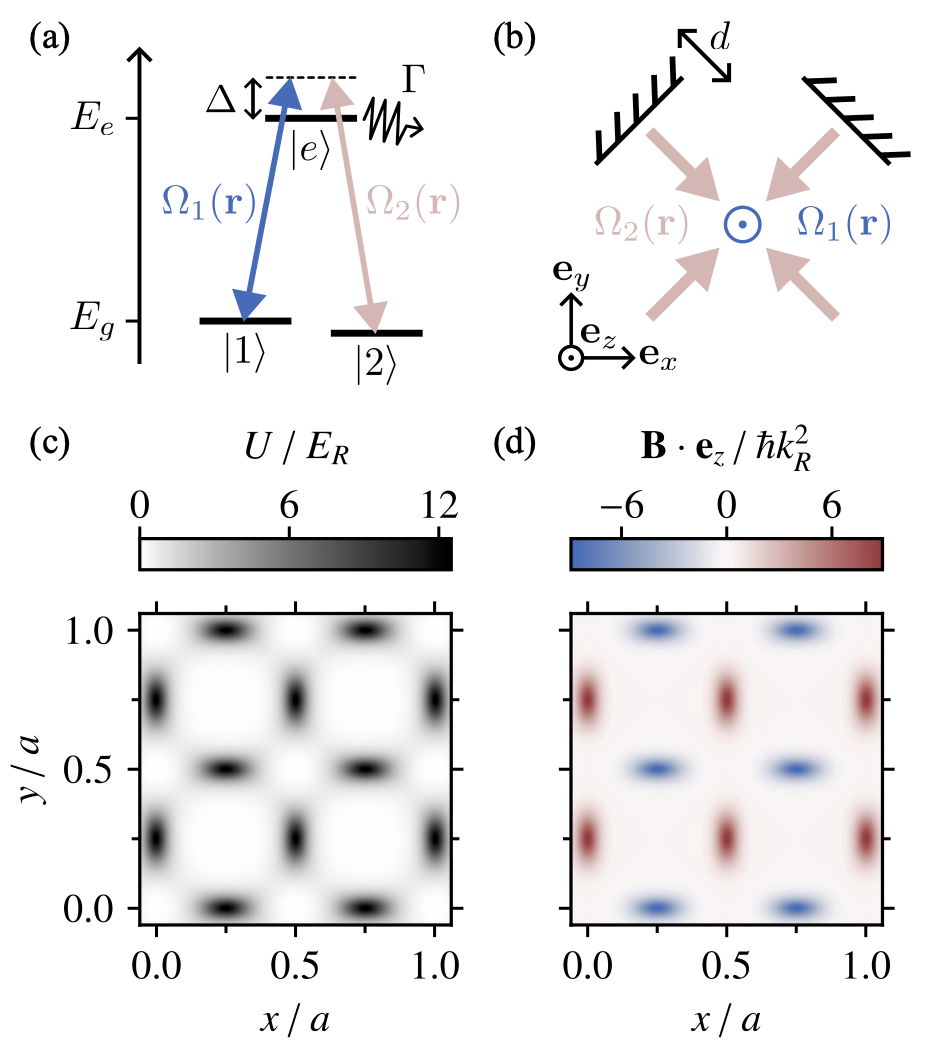
We describe a two-dimensional optical lattice for ultracold atoms with spatial features below the diffraction limit created by a bichromatic optical standing wave. At every point in space these fields couple the internal atomic states in a three-level Lambda coupling configuration. Adiabatically following the local wavefunction of the resulting dark state yields a spatially uniform Born-Oppenheimer potential augmented by geometric scalar and vector potentials appearing due to spatially rapid changes of the wavefunction. Depending on system parameters, we find that the geometric scalar potential can interpolate from a 2D analogue of the Kronig-Penney lattice, to an array of tubes with a zig-zag shaped barrier. The geometric vector potential induces a spatially periodic effective magnetic field (the Berry’s curvature) that can be tuned to cause destructive interference between neighboring tubes, thereby decoupling them at a critical point in parameter space. We numerically investigate the energy spectrum including decay from the excited state, and find that the adiabatic approximation is sound for strong coupling strengths, leading to negligible loss in the dark state manifold. Furthermore, the spectrum is well-described by a non-Hermitian tight binding model with on-site losses, and hopping characterized by both loss and, surprisingly, gain.