Dynamical instability of 3d stationary and traveling planar dark solitons

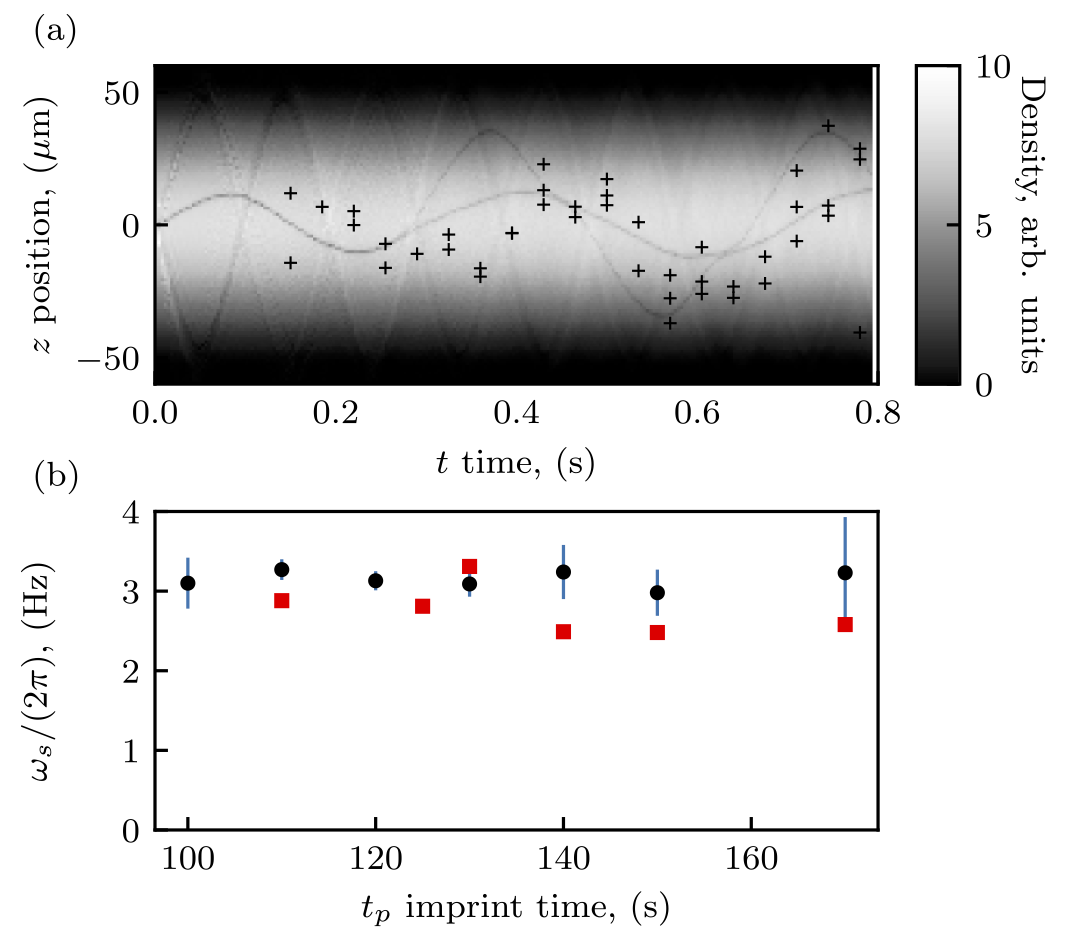
Here we revisit the topic of stationary and propagating solitonic excitations in self-repulsive three-dimensional (3D) Bose–Einstein condensates by quantitatively comparing theoretical analysis and associated numerical computations with our experimental results. Motivated by numerous experimental efforts, including our own herein, we use fully 3D numerical simulations to explore the existence, stability, and evolution dynamics of planar dark solitons. This also allows us to examine their instability-induced decay products including solitonic vortices and vortex rings. In the trapped case and with no adjustable parameters, our numerical findings are in correspondence with experimentally observed coherent structures. Without a longitudinal trap, we identify numerically exact traveling solutions and quantify how their transverse destabilization threshold changes as a function of the solitary wave speed.