Synthetic Matter
Measurement. Science is rooted in measurement: it is from measurements, as unified by theory, that understanding is born. Our comprehension of the universe is therefore bounded by our ability to observe and shaped by human creativity. Scientific progress is driven by the identification of new physical systems and measurement techniques, leading to new conceptual understanding. Our experiments use systems of ultracold neutral atoms, quantum gases, that make quantum physics manifest in the laboratory. Many properties of these systems can be understood in the intellectual context of many-body physics which describes systems from the commonplace such as crystals, fluids, and semiconductors, to the extreme such as superconductors, quantum Hall systems, and neutron stars. Many-body physics asks how the properties of individual components — atoms, electrons, nucleons — give rise to the observed macroscopic phenomena.
Ultracold atoms are a very different sort of system than conventional materials, composed of a few hundred to a few hundred million atoms, with densities ranging from 1012 cm-3 to 1015 cm-3, and at temperatures from below 1 nK to a couple uK. These atomic systems are unique in the simplicity of their underlying Hamiltonian along with a singular capacity for controlling and engineering their quantum degrees of freedom.
Our experiments — inspired by the on-going theory efforts of our collaborators world-wide — take place on three distinct apparatuses: RbK, focusing on artificial gauge fields for atomic Bose and Fermi gases; RbChip, creating spin-dependent forces without light; and RbLi, designing long range interactions mediated by particle exchange.
In addition in collaboration with Dr. Justyna Zwolak in the Information Technology Laboratory at NIST, we are exploring the application of machine learning to control, analysis and exploration in quantum experiments.
Postdoc fellowship openings. Postdoc applications are always welcome! For fellowship options, consider: the JQI Experimental postdoc program (Applications due in Feb.); NIST NRC postdoc program: candidates must be US citizens within 5 years of Ph.D. (Applications will be due in Feb. and Aug. Candidates with an interest in experiment should contact Spielman while those with an interest in machine learning should contact Zwolak). In all cases, contact should be made well in advance of these deadlines.
-
Dynamical structure factor from weak measurements
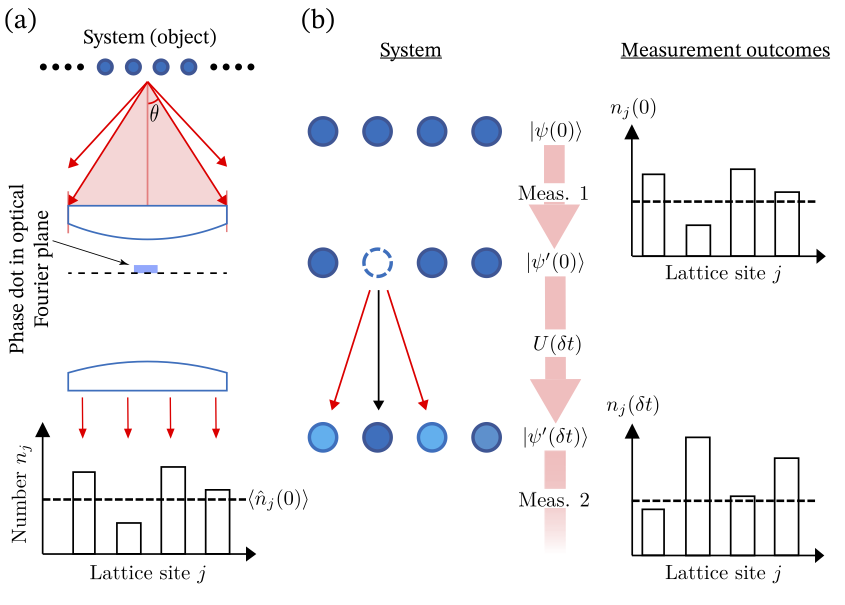
Much of our knowledge of quantum systems is encapsulated in the expectation value of Hermitian operators, experimentally obtained by averaging projective measurements. However, dynamical properties are often described by products of operators evaluated at different times; such observables cannot be … Dynamical structure factor from weak measurements Read More »
-
Dario D’Amato takes home top poster

At the 2025 Early Career Poster Presentation, Dario took home the “Most Outstanding Poster in Physics” with his poster Nondestructive Characterization of Cold Atomic Clouds with Machine Learning!
-
JQI features Mingshu’s turbulence result!

https://jqi.umd.edu/news/mysteriously-mundane-turbulence-revealed-2d-superfluid
-
Dr. Guilherme de Sousa is the master (equation) of the universe
Congratulations Guilherme!
-
Many-body phases from effective geometrical frustration and long-range interactions in a subwavelength latticeKolmogorov Scaling in Turbulent 2D Bose-Einstein Condensates
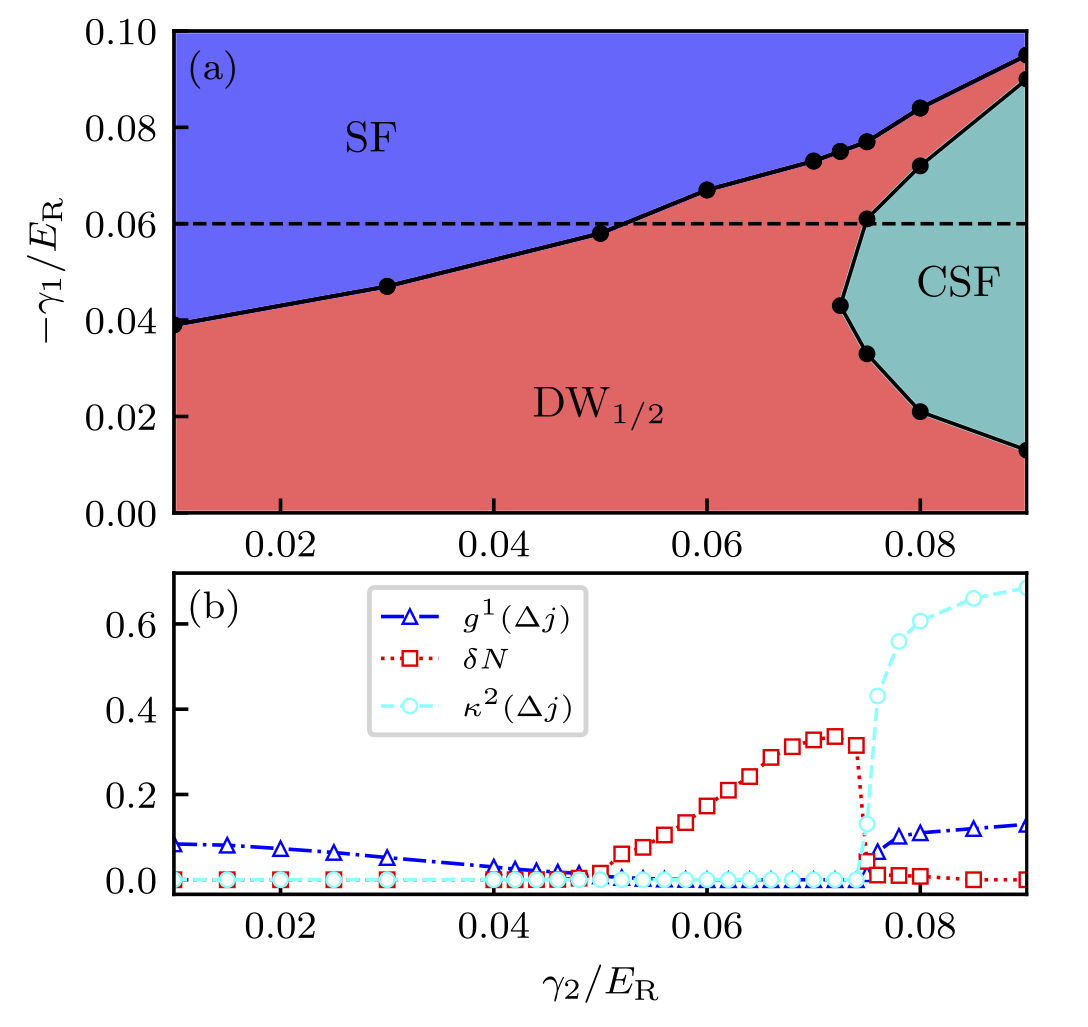
Geometrical frustration and long-range couplings are key contributors to create quantum phases with different properties throughout physics. We propose a scheme where both ingredients naturally emerge in a Raman induced subwavelength lattice. We first demonstrate that Raman-coupled multicomponent quantum gases … Many-body phases from effective geometrical frustration and long-range interactions in a subwavelength latticeKolmogorov Scaling…
